Auf Vorrat lernen oder erst wenn man es braucht?
In der Schule läuft das doch so: Man lernt Potenzgesetze. Man übt erst die direkte Anwendung eines Gesetzes an einfachen Umformungen und tastet sich dann an zunehmend komplexere Fälle heran. Da mag ein Gesetz zum Beispiel erst nach einer gewissen Vorarbeit anwendbar sein oder es muss in seiner Umkehrung angewendet werden. Erst später kommen denn mehrschrittige Aufgaben, in denen die erlernten Techniken angewendet werden und auch sogenannte Anwendungsaufgaben. Das Vorgehen macht in gewisser Weise auch Sinn, denn würde man gleich mit den komplexen und mehrschrittigen Aufgaben beginnen, wüsste ja niemand was zu tun ist.
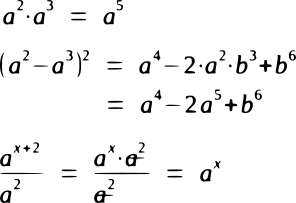
Daraus ergeben sich für mich aber zwei Probleme:
1. Die Kinder lernen zu wenig, wie man die Anwendbarkeit einer Regel erkennt.
Die meisten Kinder wissen nach der dritten Aufgabe vom selben Typ,
wie der Hase läuft. Der Lerneffekt ist ab dann vernachlässigbar.
Und trotzdem werden sie 2 Jahre später die Anwendbarkeit womöglich nicht erkennen,
da sie nicht gelernt haben, wie man ohne zu wissen, welche Regel gerade geübt wird,
erkennt, welche Regel auf die vorliegende Gleichung passt. Man muss
alles bei Bedarf nochmals wiederholen.
Manchmal gibt es gegen Ende einer Lerneinheit gemischte Aufgaben.
Ich bin aber der Meinung, dass die oft zu kurz kommen, bzw. dass nach den gleichförmigen
Übungen vorher schon die Luft raus ist.
2. Die Kinder wissen überhaupt nicht, wozu sie das lernen sollen.
Geführt vom Lehrer, der den Überblick hat,
tauchen die Kinder in einen Nebel von Regeln und Formeln.
Wenn im Regel-Unterricht meiner Schüler ein neues Thema angefangen wird,
frage ich meine Schüler, ob sie denn wissen, wo das alles hinführt.
Die Antworten reichen von »keine Ahnung«, über »mir egal« bis hin zu
»wir schreiben nächste Woche eine Test darüber« – sie
haben doch alle den selben Duktus.
Fahren auf Sicht und das Vertrauen
»Man muss die Inhalte kleinschrittig aufbereiten, sonst lernen Kinder nicht was sie lernen sollen.«
Ich denke, andersherum wird ein Schuh draus: Schüler holen sich nicht was sie brauchen weil sie 1. sich nicht selbst dazu entschieden haben, das lernen zu wollen und 2. von der Schule von Anfang an genau gesagt bekommen was sie wann zu machen haben. Wirklich eigene Ideen und eigene Prioritäten werden leider im Keim erstickt. Sie bekommen gar keine Chance, Eigeninitiative zu zeigen und zu beweisen, dass sie kein unterentwickeltes Menschen-Rohmaterial sind.
Als Kind fand ich Aussagen wie »das wirst du später brauchen« oder »das wirst du später verstehen« unerträglich und heute noch bereitet es mir Bauchschmerzen, diese Sätze als Ausflüchte zu hören – oder sie sogar selbst benutzen zu müssen. Aber die ganze Didaktik der Schulbücher und damit meist auch des Unterrichts kreist um diese beiden Sätze.
Um solche Sätze aber annehmen zu können braucht es entweder Vertrauen oder die Gewöhnung daran, dass man einfach macht, was die erwachsene Autorität für das Richtige hält, ohne ihr zu vertrauen. Zweiteres zu kultivieren ist für mich keine Option. Vertrauen allerdings entsteht im Schulkontext nur sehr selten.
Geht es auch anders?
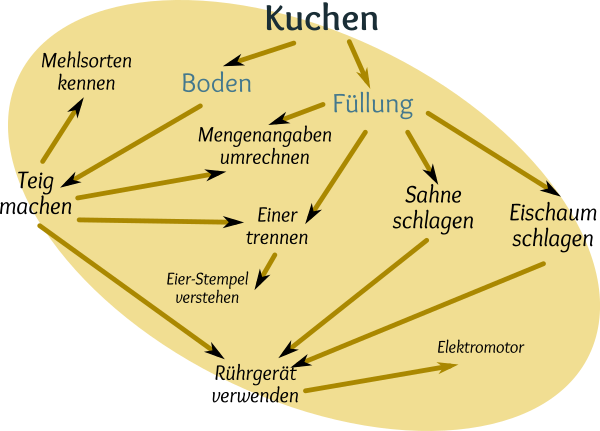
Man müsste doch wie beim Kuchenbacken einen Leitgedanken haben und diesen dann herunterbrechen auf Voraussetzungen und Einzelschritte, auf Techniken und Werzeuge die benötigt werden.
- »Wie entstehen 3D-Grafiken?«
- »Wie funktioniert die Digitalisierung von Klängen?«
- »Wie gestaltet man eine aussgekräftige Stichproben-Studie?«
Die benötigten Techniken kann man dann auch für einen Moment isoliert üben. Und Werkzeuge kann man ausprobieren, an Stellen, an denen man nichts kaputt machen kann, bis man die benötigt Sicherheit im Umgang hat. Aber man weiß immer, wofür man das alles tut.
Ich selbst habe mich nie getraut, den Mathe-Unterricht einmal von dieser anderen Seite zu betrachten: Dabei träume ich schon lange von einem Projekt, bei dem im besten Fall Kinder zusammen kommen, die sich ein bestimmtes Ziel setzen oder ein Thema vornehmen.
Dann würde man schauen, was man benötigt um dem Ziel näher zu kommen. Man würde auf Begriffe stoßen, die es zu definieren und zu erklären gilt. Man würde auf Hindernisse stoßen, für die man eine Lösung braucht. Man würde das Thema vielleicht vereinfachen wollen, weil es sonst nicht leistbar wäre. An diesem Punkt könnte ein Lehrer im Auftrag der Kinder eine nachvollziehbare Reduktion vornehmen, mit der alle einverstanden sein werden.
Wenn es um die 3D-Grafik geht würde die Kinder vielleicht lernen wollen, wie das dreidimensionale Sehen beim Menschen funktioniert und was eine Projektion ist. Man würde feststellen, dass man Symbole braucht um Orte im Raum und Orte auf dem Bildschirm beschreiben zu können. Und man würde sich klar machen, dass man einen Verfahren braucht, mit dem man die Raum-Punkte in die Ebenen-Punkte verwandelt, sodass es einer optischen Projektion entspricht.
Die klassische Vorgehensweise in der Schule ist, dass man sich vorher überlegt, welche Inhalte und Techniken die Schüler lernen sollen. Dann denkt man sich Aufgaben aus, die dazu passen. Dann lehrt man alle Grundlagen, die man für die Aufgaben braucht. An diesem Vorgang sind die Kinder aber nicht beteiligt.
Um dem Ziel also näher zu kommen, will man sich mit Geometrie und vielleicht sogar der Vektor-Geometrie beschäftigen. Aber man weiß, wie man auf das Thema gestoßen ist, inwiefern es Relevant ist und wozu es führen wird.
Und ganz wichtig: Wenn der Lehrer das Thema des Projektes vorgibt (weil er aus welchen Gründen auch immer das Thema Geometrie unbedingt unterbringen möchte), dann funktioniert das Ganze nicht mehr.
Und jetzt?
Ich würde sehr gerne erfahren, ob jemand soetwas mal probiert hat. Problematisch dabei ist, dass den Kindern schon in der Grundschule diese eine Schul-Arbeitsweise antrainiert wird. Und wenn das Wort »Geometrie« schon Schul-verseucht ist, könnte das ein Hindernis sein.
Zum Weiterlesen:
Anwendungsaufgaben sind oft an den Haaren herbeigezogen
Vielen Kindern in der Schule erscheinen die Aufgaben aus dem Mathe-Buch realitätsfern und schwachsinnig. Zurecht. Ich behaupte, das ist ein Faktor, warum sich viele Kinder mit Mathe so schwer tun. Aber muss das so sein?
Die drei Schüler-Strategien, um mit dem Mathe-Unterricht »klarzukommen«
Dumme Aufgaben, irrelevante Themen, uninteressante Probleme. Das ist Mathe-Unterricht in Kurzfassung. Ich habe in meiner Tätigkeit drei unterschiedliche Strategien beobachtet, wie Kinder in der Schule damit umgehen.