Anwendungsaufgaben sind oft an den Haaren herbeigezogen
Eigentlich ist es super, wenn im Mathe-Unterricht »Anwendungsaufgaben« gemacht werden. Es sollte ja nicht nur bei grauer Theorie bleiben.
»Die Bruchkante einer Glasscheibe wird durch folgende Parabel beschrieben…«
Auch im Kunstunterricht habe ich fragwürdige Arbeitsaufträge gesehen. Aufgabenstellung: Einen Feuervogel malen. Dazu gibt es eine Vorlage, an die sich alle lieber halten – sonst riskieren sie schlechte Noten. Einem Kind, das die Krallen nicht hinbekam, hat die Lehrerin die Krallen gezeichnet…
Umso betrüblicher ist, dass gerade anwendungsorientierte Aufgaben oft sehr an den Haaren herbeigezogen sind. Sie behandeln fiktive Probleme, die otfmals irrelevant sind in der Lebensrealität der Kinder – insgesamt unglaubwürdig. Die Kinder machen sich das zwar meist nicht bewusst – aber sie scheinen ein Gespür für unsinnige Sachen zu haben. Sehr gesund wie ich finde. Erkennbar bleibt nur eine ablehnende Haltung, Frust und nicht zuletzt ein falsches Bild der Mathematik.
Ich amüsiere mich sehr gerne mit meinen Nachhilfe-Schülern und -Schülerinnen zusammen über die ein oder andere Aufgabenstellung.
Wer sich dann bei einer solchen Anwendungsaufgaben mit kreativen Lösungen mal so richtig austoben möchte wird allerdings doch bald ausgebremst: Es geht ja darum, die Aufgaben mit den Mitteln zu Lösen, die im Unterricht zuvor eingeführt wurden. Ein für viele Kinder naheliegender Ansatz, das Problem zum Beispiel einfach durch Probieren zu lösen, ist in der Regel nicht zulässig, damit falsch und wird negativ gewertet.
Schüler: ich probier‘s einfach aus!
Ich: Stell dir vor, du willst einen Anhänger mieten und musst dir vorher überlegen, ob sie rein passt.
Schüler: Wenn sie nicht rein passt, säge ich sie ein Stück ab!
Ich: Die Leiter war teuer und sollte doch am besten so lange bleiben wie sie ist.
Schüler: Ich lasse sie einfach überstehen und hänge eine rote Fahne dran. Mir doch egal. Ladungssicherung natürlich nicht vergessen!
Ich: Okay, du hast gewonnen!
Warum sind die Aufgaben nicht realistischer?
Die naheliegenste Forderung: Lasst die Kinder doch realistische Aufgaben lösen! Die Statik einer Brücke, die Mathematik einer echten Medikamentenstudie oder die optimale Milchtüte – zum Beispiel.
Abgesehen davon, dass auch solche Aufgaben die meisten »Pubertiere« nicht vom Hocker reißen werden, wäre das zumindest mal was. Aber hierbei bekommen wir noch ganz andere Probleme:
Allein das Beispiel mit der Leiter ist in Wirklichkeit komplexer als der »Satz des Pythagoras«:
Will man die Fragestellung wirklich ernst nehmen und mathematisch lösen, genügt es nicht, nur die Diagonale zu berechnen. Bei dem genannten Beispiel wäre das Resultat so knapp, dass man möglicherweise die Dicke und die Form der Leiter mit berücksichtigen müsste, was zu einer deutlich komplizierteren, aber realistischen Aufgabe führt.
Mit der Verwendung eines grafischen Taschenrechners werden theoretisch realistischere Aufgaben im Schulkontext möglich – aber für diesen Abiturjahrgang hat man ihn schon wieder abgeschaft, bevor man sein Potezial richtig ausschöpfen konnte...
Die Aufgaben in den Schulbüchern sind also in erster Linie vereinfacht. Manchmal so sehr, dass das »Problem« dabei verloren geht. Nur wenige sind in der Schule dazu in der Lage, hinter diesen modellhaften Aufgaben ein größeres ganzes zu sehen, sie wie ein Fenster zur Real-Mathematik zu sehen, die unser tägliches Leben gewaltig mitbestimmt.
Gibt es auch realistische Aufgaben?
Als ich selbst noch Aufgabensteller war, hatte ich große Mühe, sinnvolle und doch machbare Aufgaben zu erstellen. Zumal realistische Projekte, bei denen eine Lösung am Ende auch eine wirkliche Bedeutung hätte, leider zu viel Zeit in Anspruch genommen hätten. Ich möchte aber dennoch eine Aufgabe präsentieren, die für mich in die richtige Richtung geht:
Ist die reale Milchtüte hinsichtlich des Materialverbrauchs optimiert? Begründen Sie.«
Die optimale Milchtüte, ist eine ziemlich gelungene Aufgabe, auch wenn für meinen Geschmack noch zu viel vorgegeben ist. Sie führt allerdings zu einer Gleichung, die die Kinder in der Schule nicht analytische lösen können. Ohne technische Unterstützung wäre das Lösen sehr mühsam.
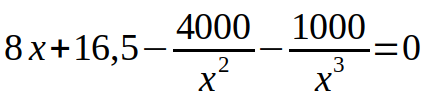x ist dabei dann die optimale Breite der Milchtüte.Die Frage nach der Relevanz der Thematik für das Kind vernachlässige ich an dieser Stelle.
Auch eine realistische Aufgabe (auch wieder für den einzelen Schüler nicht zwangsläufig interessant): »Kann man sterben wenn man den "Gefleckten Schierling" (Conium maculatum) isst? Wieviel müsste man davon essen?«
Und jetzt?
Aber warum die ganze Aufregung? Es sind doch nur Schulaufgaben!
Ich bin der Überzeugung, dass die Tatsache, dass Kinder diesen Pseudo-Problemen ausgesetzt sind, nachhaltige Auswirkungen hat. Zum einen erzeugt das Radar für unehrliche Dinge, das Schulkinder sich nur langsam abtrainieren, zu latentem Frust und steigender Demotivation. Zum anderen verfestigt das ganze den Verdacht, man habe es nicht mit Bildung zum selbstbestimmten Menschen zu tun, sondern nur um das erbringen von Leistungsnachweisen.
Zum Weiterlesen:
Auf Vorrat lernen oder erst wenn man es braucht?
Oftmals werden Verfahren und Regeln zunächst losgelöst von ihren Anwendungen sehr ausführlich trainiert. »Das braucht ihr später« - lautet die Begründung des Lehrers. Reicht das als Motivation?
Die drei Schüler-Strategien, um mit dem Mathe-Unterricht »klarzukommen«
Dumme Aufgaben, irrelevante Themen, uninteressante Probleme. Das ist Mathe-Unterricht in Kurzfassung. Ich habe in meiner Tätigkeit drei unterschiedliche Strategien beobachtet, wie Kinder in der Schule damit umgehen.